如何利用B-S模型计算可转债的期权价值?
来源:雪球App,作者: 大象咖啡,(https://xueqiu.com/8188497048/143871579)

整个世界都在下坠!这个时候最好的做法,就是暂时屏蔽市场,静下心来,忘掉“股灾,危机,萧条”之类的词汇,自己思考思考;或者泡一杯咖啡,看看书,学习学习。
本篇笔记我们来聊聊怎么算可转债的期权价值。
1、可转债的内在价值包含哪些
做可转债的朋友,一般非常关注 可转债价格 与 转股溢价率 这两个量。通过这两个量,我们会大概判断出,如果可转债价格低,其纯债价值就高;如果转股溢价率低,那么其转股价值就高。
上面的方法是定性的判断,那么,我们可不可以定量地计算出可转债的 内在价值 呢?有了内在价值,就可以制定一个简单的策略:若当前可转债价格低于其内在价值,那么买入;价格若超过内在价值,就卖出。
现在的问题是如何计算内在价值。我们知道,可转债首先是债券,然后在其上附上了一个看涨期权。所以, 可转债的内在价值 = 纯债价值 + 看涨期权价值 。
纯债价值的计算相对简单,就是将未来利息与期末偿还本金按选定的贴现率贴现就行(如,同等级债券收益率)。有很多文章介绍纯债价值的计算,这里不另外说了。在东方财富网站 网页链接 输入可转债代码或简称也可以查到。
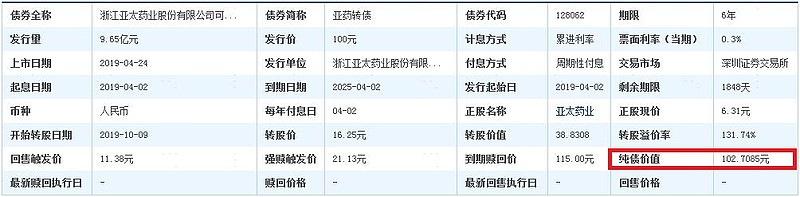
下面重点来谈谈可转债期权价值的计算。本文利用一个经典的方法: Black-Scholes(B-S)模型 。该模型由罗伯特·默顿(Robert Merton)和斯坦福大学教授迈伦·斯克尔斯(Myron Scholes)创立,他们也因此获得了1997年的诺贝尔经济学奖。
2、B-S模型
B-S模型基于一个核心思路是: 计算出可转债到期时正股股价的分布;根据这个分布求出期权价值(或者转股价值)的期望;最后将这个期望按无风险利率贴现到现在即得 。
B-S模型是从当下开始按连续时间进行积分,得到到期时正股股价的分布。需要随机微积分的知识,在这里就不详细展开了,直接上公式:
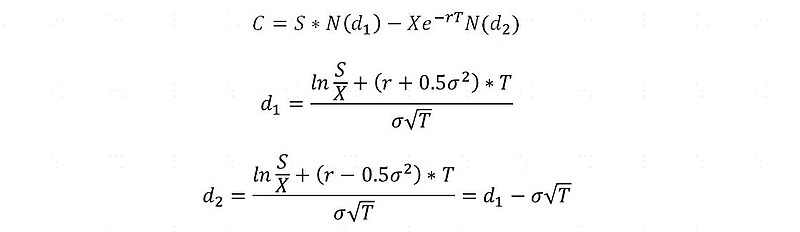
我们看看上面公式中出现的变量:
(1)C :当前看涨期权的价值,这个是正股的期权价值(最后要转成可转债的)。
(2)S :正股当前的价格,这个容易取到。
(3)X :期权的行权价,就是可转债的转股价格,这个是给定的。
(4)T :当前到转债到期日的时间,换算成以年为单位。
比如,当前可转债到期日还有452天,那么T=452/360=1.26。分母中你也可以取365,习惯上是360。
(5)r :无风险利率,且为连续复利下的年化收益率。
无风险利率你可以参考 国债收益率 、 Shibor 、或者 204001 。假设现在的无风险年化收益率为2.48%,怎么换算到连续复利下的年化收益率呢?通过下面这个公式:
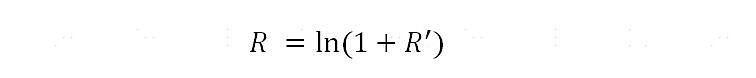
其中,R’是年化收益率,R是连续复利下的年化收益率。比如当R=2.48%,那么根据上面公式得到R’=2.45%。
(6)σ :正股的年化收益率标准差。
好吧,这个有点难理解。收益率的标准差实际上指示了收益率的波动程度,一般可以看成股票的历史波动率。年化收益率标准差怎么算呢?我们可以先把股票每日的收益率(就是每日涨跌幅)数据拉下来,比如拉个5年的数据,然后计算这一组数据的标准差。这里计算的标准差是 日收益率标准差 。最后,通过下面的公式得到 年化收益率标准差 :
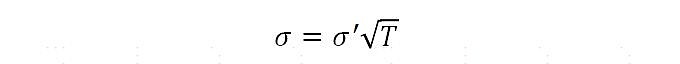
其中,σ’是日收益率标准差;σ是年化收益率标准差;T一般取值250,大概是一年交易日个数。
(7)N(d) :标准正态分布<=d的累积概率。比如标准正态分布的均值为0,那么N(0)=0.5。这个计算过程在很多数据分析工具中会提供的(R,Python等)。
重要的一步:
上面算出来的C其实是股票的看涨期权价值,我们还要换算成可转债的期权价值,利用下面的公式:
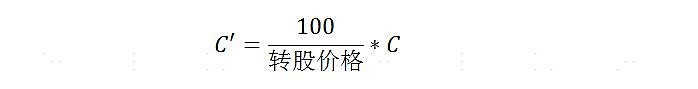
其中,C’就是我们最终求得的可转债的期权价值。
根据上面的解释,我们都能有办法得到公式中的变量值,那么就可以计算出当下的期权价值了。
3、一个栗子
下面通过栗子来算一算会深刻一些。
下表是截止2020年3月12日收盘, 海澜转债 (110045.SH)的相关数值:
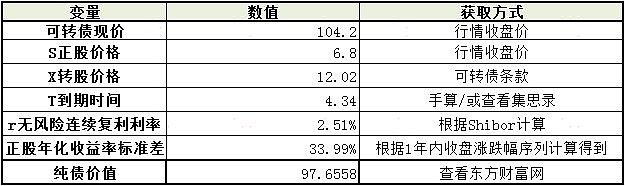
(如果需要 海澜之家 近两年日收盘价数据做验证,可以关注公众号“大象咖啡屋”,后台回复“600398”即可。)
下面就是代入上面的数值计算啦:
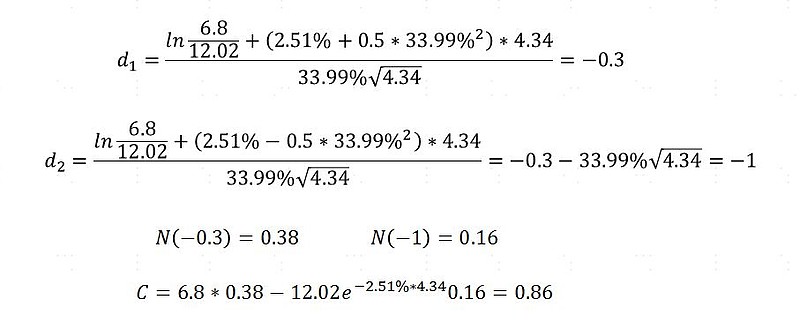
算出C=0.86,下一步就是算出 可转债的期权价值 ,即C’=(100/12.02)*0.86=7.15。通过计算或者查看东方财富网,得到 纯债价值 为97.66。
因此可转债在2020年3月12日收盘后的 内在价值 为 7.15+97.66 = 104.81。可转债收盘价为104.2,看来还是非常接近理论上的内在价值的。
4、不得不说的缺点
B-S模型是目前计算期权价值比较理想的模型,但模型计算出来的永远是理论价值,不能完全对应实际的内在价值。
另外,本文的经典B-S模型,更确切地只能应用在 非奇异的欧式期权 的价值计算上。
这里有两个条件: 非奇异 与 欧式 (这两个概念的深入知识不具体展开了)。从本质上来说,可转债其实都不满足。可转债可能像美式期权那样提前“行权”,在到期日之前就强行赎回或者回售等,比如去年的 平安转债 。另外,可转债毫无疑问是奇异期权,比如,它能下修转股价。
还有,B-S模型本身就基于一些较强的假设,比如 证券的无限可分性 、 无套利空间 、 无摩擦成本 等。所以理论值与实际不会完全匹配。
所以,小伙伴们不能完全依赖于B-S模型算出的期权价值,将其作为参考是更明智的选择。
5、总结
本文介绍了B-S模型计算可转债期权价值的方法。小伙伴们只要得到公式中变量的值,然后代入计算即可。
另外,本文也提到了这种方法存在不足,应用上是受限的。小伙伴们也不要完全依赖B-S模型算出来的值。
后面有机会,我会进一步介绍B-S模型的改进版,用来处理奇异期权与美式期权。另外,还有两个不错的工具: 二叉树定价模型 与 蒙特卡洛方法 。这两个工具可以加入对奇异期权与美式期权的处理过程。喜欢写程序的朋友,我更推荐 蒙特卡洛方法 ,中间过程修正比较灵活。
【推荐】
喜欢可转债投资的朋友,可以关注这几位老师的雪球号: @饕餮海 @持有封基 @DAVID自由之路
最后推荐两本书:
对B-S模型感兴趣的朋友可以参考John Hall的《期权、期货及其他衍生品》(期权入门必读)。
对B-S模型背景故事感兴趣的朋友可以读一读Emanuel Derman的《宽客人生》。



