一、绪论

这个专栏的内容不涉及高深的Kriging预测模型知识，仅为本人在本科毕业设计过程中学到的整体思路和部分代码实践，以供抛砖引玉，为刚接触Kriging预测模型的人提供一点思路。

代理模型法是 20 世纪下半叶兴起的新型可靠性分析方法。在研究对象涉及到大量随机变量时，难以得到对系统的精确解析函数，或者多种随机变量存在不明确的复杂耦合关系，都使得直接解析复杂费时。代理模型旨在建立一种近似的数学模型，来简化可靠性分析的过程。

现有的代理模型中， Kriging 模型不仅可以给出预估值，还能给出预估值的误差估计，这是 Kriging 模型区别于其他代理模型的显著特点。

对于初学者而言，可以将Kriging模型理解成一个黑箱，将大量的原始数据输入Kriging模型，并调节参数后，该模型即可自动分析数据间的联系，并通过待预测数据与已知数据间的联系密切与否给出结果。

笔者的毕业论文是对某齿轮机构的可靠性进行分析，在初期对Kriging模型可以说一头雾水，且丝毫没有意识到对模型的认知深度并非毕业设计的重点内容，因此浪费了许多时间。

二、Kriging模型介绍

Everything is related to everything else, but near things are more related to each other.

上面这句话是地理学第一定律。这句话指出，世间万物都存在联系，且存在的联系强度与它们之间的的距离呈正相关。Kriging模型的预测原理便是基于这个基本假设。

根据地理学第一定律，人们最早应用于采矿等地理学预测方面的理论相当简单，为反距离插值法。所谓反距离插值法，是指在 已知地面上 的 几组二维坐标 以及这 几组二维坐标 对应的 属性值 （如某个坐标下的矿物品级）的情况下，对某 待预测坐标 的 属性值 按照距离的反比进行插值。

反距离插值法的算法相当简单，如下所示。

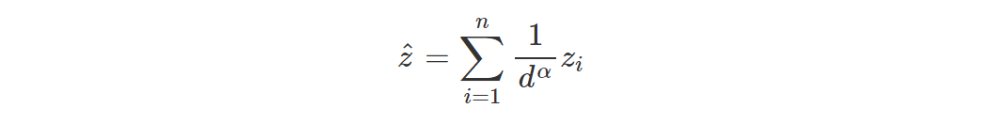
(2.1)式中的 z 表示已知的n组二维坐标对应的 属性值 ，d表示已知的 n组二维坐标中 的任意一组，与 待预测属性值所在坐标 的距离。可见，通过这种反比加权求和的形式即能简单地基于已知数据进行插值来预测。

但是(2.1)式也有许多问题，例如在α的取值往往取决于经验之谈，例如该式本身用于用于预测的精度不尽如人意等等。

Kriging模型的思想最早由南非采矿工程师Krige于1951年提出，起初用于对矿物分布的预测，随后法国数学家Matheron进行了完善并形成了完整的数学理论。具体的模型推导详见文末的文章推荐。

详细的模型推导也并不建议本科阶段去钻研，一是大多数的本科院校其毕业论文也不会要求在模型理论方面去做过多的研究以及改善，二是模型的推导过程中存在很多本科阶段完全没接触的数学知识，包括矩阵求导等。笔者当时啃了近两个星期的模型推导，但是也只是勉强看明白了预测部分，在预测误差部分几乎是一点进展都没有。

当然这也可能与笔者数一将将考到及格线附近拉跨的数学水平有关。

接下来笔者将主要着墨于Matlab软件中Kriging模型的DACE工具箱的简单使用。

1.DACE工具箱的简介

该工具箱是应用于Matlab软件的Kriging模型代码实现集合文件夹，其中包括Kriging模型的预测器、几种相关函数、几种回归模型，以及一些示例数据。该工具箱来自丹麦技术大学2002年发表的一篇文章。

工具箱中还包括一份命名为dace的PDF文件，这个PDF文件中全面地介绍了Kriging模型的推导以及工具箱Kriging模型代码实现过程中出现的诸多函数的解释，可以说是DACE工具箱详尽的使用说明书

这份PDF文件是英文写成，对于笔者这种低分过6级的本科生来说当时啃起来十分吃力，更不用说其中Kriging模型推导过程专业的数学术语了，幸运的是在CSDN上存在一份译文，但是译者应该也并不是业内人士，部分名词在笔者印象里也出现了一些不太标准的现象，但仍是一份好译文。

2.样本抽样

对于Kriging模型而言，需要足够大的样本数量以及样本具有足够的代表性来保证建立的预测模型之精度。Matlab中自带有拉丁超立方抽样函数，该抽样方法的特点在于存在多维变量的情况下，对每个维度单独进行随机抽样，并组合成一组多维随机数据以保证随机性。

代码如下

clc

clear all

close all

cst_Mu_Sigma = [3 25 31350;0.2 1 3000]'; Mu表示正态分布均值Sigma表示正态分布方差

Mu = cst_Mu_Sigma(:,1);

Sigma = cst_Mu_Sigma(:,2);

D = size(Mu,1);

Covariance_Matrix = zeros(D,D);

for i = 1:D

Covariance_Matrix(i,i) = Sigma(i)^2;

end

N = 10;

UB = Mu + 3*Sigma;

LB = Mu - 3*Sigma;

X = lhsnorm(Mu, Covariance_Matrix, N);

figure(6)

plot(X(:,1),X(:,2),'*')

代码表示，在三个维度的均值分别为3，25，31350、三个维度的方差分别为0.2，2，3000时，按照正态分布拉丁超立方抽样法抽取10组数据，并在样本空间中用*表示出抽样分布情况。
3.构成Kriging模型的样本库

通过 readmatrix 函数即可将Matlab软件外的表格数据读取到软件的矩阵当中。

4.构建Kriging模型

若已经得到样本库，则可以通过读取样本库矩阵的列矩阵来生成S随机变量矩阵和Y样本响应值矩阵。S和Y列数不一定相等，但行数必定相等。

调用DACE工具箱中的dacefit函数，设置theta、lob以及upb三个参数，即可生成Kriging模型。代码如下：

theta = [10 10 10]; lob = [1E-1 1E-1 1E-1]; upb = [20 20 20];

[dmodel, perf] = dacefit(S, Y, @regpoly1, @corrgauss, theta, lob, upb);

工具箱作者在说明书中明确指出关于theta、lob以及upb三参数一般无需变动。

dacefit函数中的第三和第四个变量分别是回归函数和相关函数，一般工程中用的都是高斯相关函数。

5.调用预测器

[y]=predictor(u,dmodel)

上述代码得到的矩阵便是预测结果矩阵。

Kriging模型的整个使用部分的代码相当简单，如前所述基本可以分为四个部分。前文所述的四个部分使用的代码虽然全来自于笔者的本科毕业论文，但截取后也基本没有前后关系。

总结下来，Kriging模型的基本使用方法便是

1需要搞到足够多的样本，包括基本数据和属性值，

2建立模型

3输入新的基本数据，并进行预测

三、参考文献

1. CSDN：克里金(Kriging)插值的原理与公式推导_转

2. CSDN：克里金(kriging)模型的推导详解

3. 知乎：克里金(Kriging)模型详细推导

4. 豆丁网： 毕业论文（设计）基于kriging模型的结构可靠性分析及寿命估算

5. 笔者的毕业论文秒链：5547ac6294c07cdc7731cff6603fa292#7536fad761eee2c31ea42b50a28527a8#1379925#毕业论文.docx

这个专栏写于读研一之前的8月份，此时距离写完毕业论文已经过去将接近两个月，对细节方面的内容已经不甚明了，如有笔误和理论知识的错误还望海涵。

若读者还有什么疑惑之处可以在评论区留言，笔者基本上也不咋会其实。