Python 实现巴特沃斯滤波器_巴特沃斯滤波器python_柳叶吴钩的博客

3 python代码实现

由于笔算IIR滤波器参数较为复杂，本代码采用scipy中的butter滤波器直接计算出相应的参数，python实现IIR滤波算法较为简单，在该代码中被略去，有需要者，私聊博主。
感兴趣的读者可以对比计算得到的滤波器参数和教程中计算得到的参数，会发现其值与教材中计算的相差无几。
import numpy as np
import math
from sympy import *
from scipy import signal
import scipy 
import matplotlib
import matplotlib.pyplot as plt
from scipy.fftpack import fft,ifft
plt.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] =False
#设计一巴特沃斯带通滤波器
#通带下限频率150Hz
#通带上限频率200Hz
#下阻带下限频率100Hz
#上阻带下限频率250Hz
#通带衰减不大于3dB
#阻带衰减不小于18dB
#采样间隔T = 0.001s
fp_l = 150
fp_h = 200
fs_l = 100
fs_h = 250
T    = 0.001
fs   = int(1/T)
wp_l = 2*np.pi*fp_l * T
wp_h = 2*np.pi*fp_h * T
ws_l = 2*np.pi*fs_l * T
ws_h = 2*np.pi*fs_h * T
Wp_l = np.tan(wp_l/2)
Wp_h = np.tan(wp_h/2)
Ws_l = np.tan(ws_l/2)
Ws_h = np.tan(ws_h/2)
#计算中心频率
W_o = Wp_l*Wp_h
#计算通带带宽
W_BW = Wp_h-Wp_l
#对频率指标归一化
H_sl = Ws_l/W_BW
H_sh = Ws_h/W_BW
H_pl = Wp_l/W_BW
H_ph = Wp_h/W_BW
H_o  = H_pl*H_ph
#进行频率变换
L_p  = (H_ph**2 - H_o)/H_ph
L_sl = (H_sl**2 - H_o)/H_sl
L_sh = (H_sh**2 - H_o)/H_sh
if(abs(L_sh)<abs(L_sl)):
    L_s = L_sh
else:
    L_s = L_sl
#print(L_s)
#设计模拟低通滤波器
G_p = 3
G_s = 18
#确定滤波器阶数
N = math.log(np.sqrt(10**(G_s/10)-1),10)/math.log(L_s,10)
print(N)
#取大于N的数作为滤波阶数
#if(int(N)>N):
#    N=int(N)/2
#else:
#    N = (int(N)+1)/2
if(int(N)<N):
    N=int(N)+1
print(N)
fl = fp_l
fh = fp_h
Wn = [fl*2/fs,fh*2/fs]
x=np.linspace(0,1,fs)
#设置需要采样的信号
signal_array = np.sin(2*np.pi*500*x)
for i in range(10):
    if 100*i != 500:
        signal_array+=np.sin(2*np.pi*100*x*i)#+np.sin(2*np.pi*175*x)+np.sin(2*np.pi*350*x)+np.sin(2*np.pi*500*x)
noise_size = len(signal_array)
noise_array =  np.random.normal(0, 2, noise_size)
mu = 0
sigma = 0.12
import random
noise_array = random.gauss(mu,sigma)
adc_value=[]
test = []    
for i in range(noise_size):
    adc_value.append(random.gauss(mu,sigma))
    test.append(1)
#signal_array= np.array(adc_value) + np.array(test)
signal_size = len(signal_array)
K = np.arange(signal_size)
T1 = signal_size/fs
frequency_array = K/T1/10
#计算源信号的FFT
signal_fft=fft(signal_array)                     #快速傅里叶变换
signal_fft_abs=abs(fft(signal_array))                # 取模
signal_fft_abs_norm=abs(fft(signal_array))/((len(signal_array)/2))           #归一化处理
signal_fft_abs_norm_half= signal_fft_abs_norm[range(int(len(signal_array)/2))]  #由于对称性，只取一半区间
signal_fft_abs_size =np.arange(len(signal_array))        # 频率
IIR_filter=filter()
#计算巴特沃夫滤波器参数
b_weight,a_weight = scipy.signal.butter(N, Wn, btype='bandpass')
#利用计算得到的滤器参数进行滤波
IIR_Output =  IIR_filter.IIR_F(signal_array,a_weight,b_weight)
IIR_Output_Size = len(IIR_Output)
plt.figure(1)
plt.subplot(221)
plt.title('原始信号')  # 定义标题
plt.plot(signal_array[0:1000],'g') 
plt.subplot(222)
plt.title('滤波后的信号')  # 定义标题
#t=np.sin(2*np.pi*500*x)
#plt.plot(t[0:1000],'g') 
#plt.plot(signal_array[0:1000],'g') 
plt.plot(IIR_Output[0:1000],'b') 
plt.show()
IIR_Output = np.array(IIR_Output)
IIR_Output_fft=fft(IIR_Output)                     #快速傅里叶变换
IIR_Output_fft_abs=abs(fft(IIR_Output))                # 取模
IIR_Output_fft_abs_norm=abs(fft(IIR_Output))/((len(IIR_Output)/2))           #归一化处理
IIR_Output_fft_abs_half = IIR_Output_fft_abs_norm[range(int(len(IIR_Output)/2))]  #由于对称性，只取一半区间
IIR_Output_fft_abs_size = np.arange(len(IIR_Output_fft_abs_norm))        # 频率
plt.subplot(223)
plt.title('原始信号FFT')  # 定义标题
plt.plot(signal_fft_abs_size[0:1000],signal_fft_abs_norm[0:1000],'g') #显示原始信号的FFT模值
plt.subplot(224)
plt.title('滤波后的信号FFT')  # 定义标题
plt.plot(signal_fft_abs_size[0:1000],IIR_Output_fft_abs_norm[0:1000],'r',label='FFT') 
#plt.legend('滤波后信号FFT')
plt.show()
plt.figure(2)
w, h = signal.freqz(b_weight, a_weight)
plt.semilogx(w, 20 * np.log10(abs(h)),markersize = 15)
plt.title('巴特沃斯滤器频率响应')
plt.xlabel('Frequency [radians / second]')
plt.ylabel('Amplitude [dB]')
plt.margins(0, 0.1)
plt.grid(which='both', axis='both')
plt.axvline(100, color='green') # cutoff frequency
plt.show()
4 运行结果
 
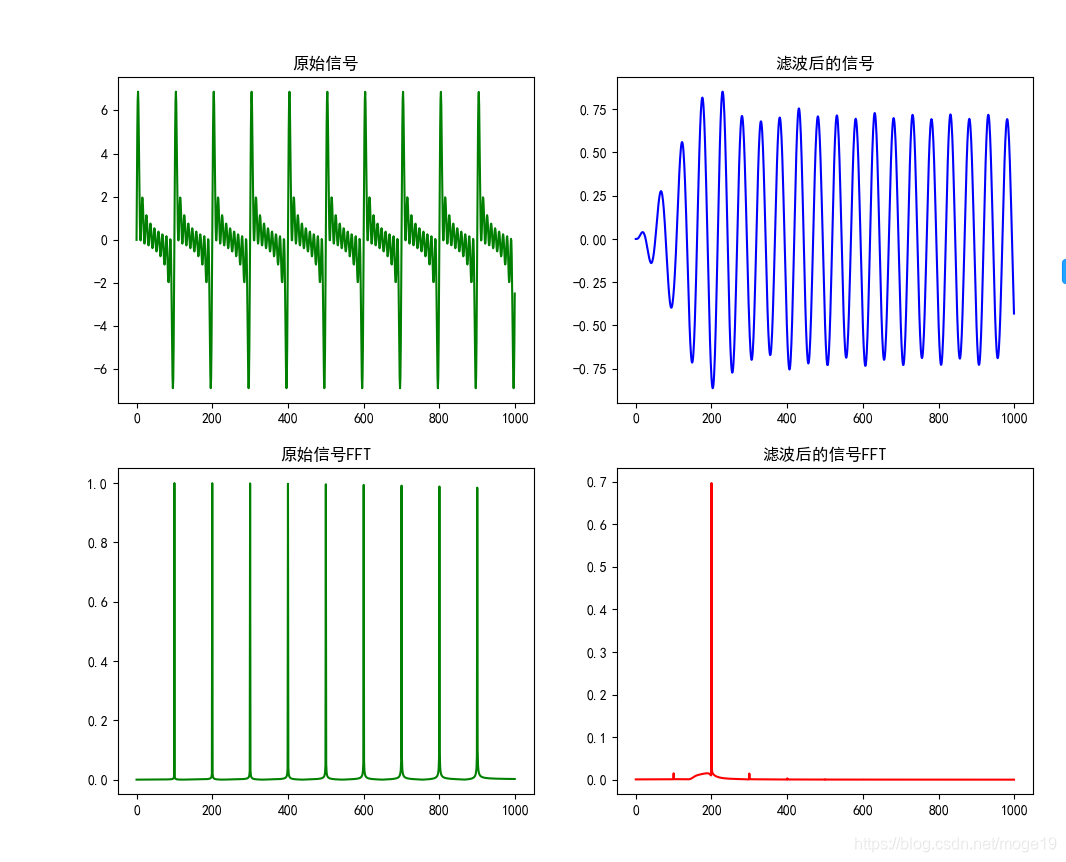
通过对比下图，可见滤波后的频谱图显示无关频道的信号得到有效衰减，但是滤波后的信号，仍然没有得到较好的信号信息，这里可以采用零相移滤波器来实现可得到更好的滤波效果。
 
 
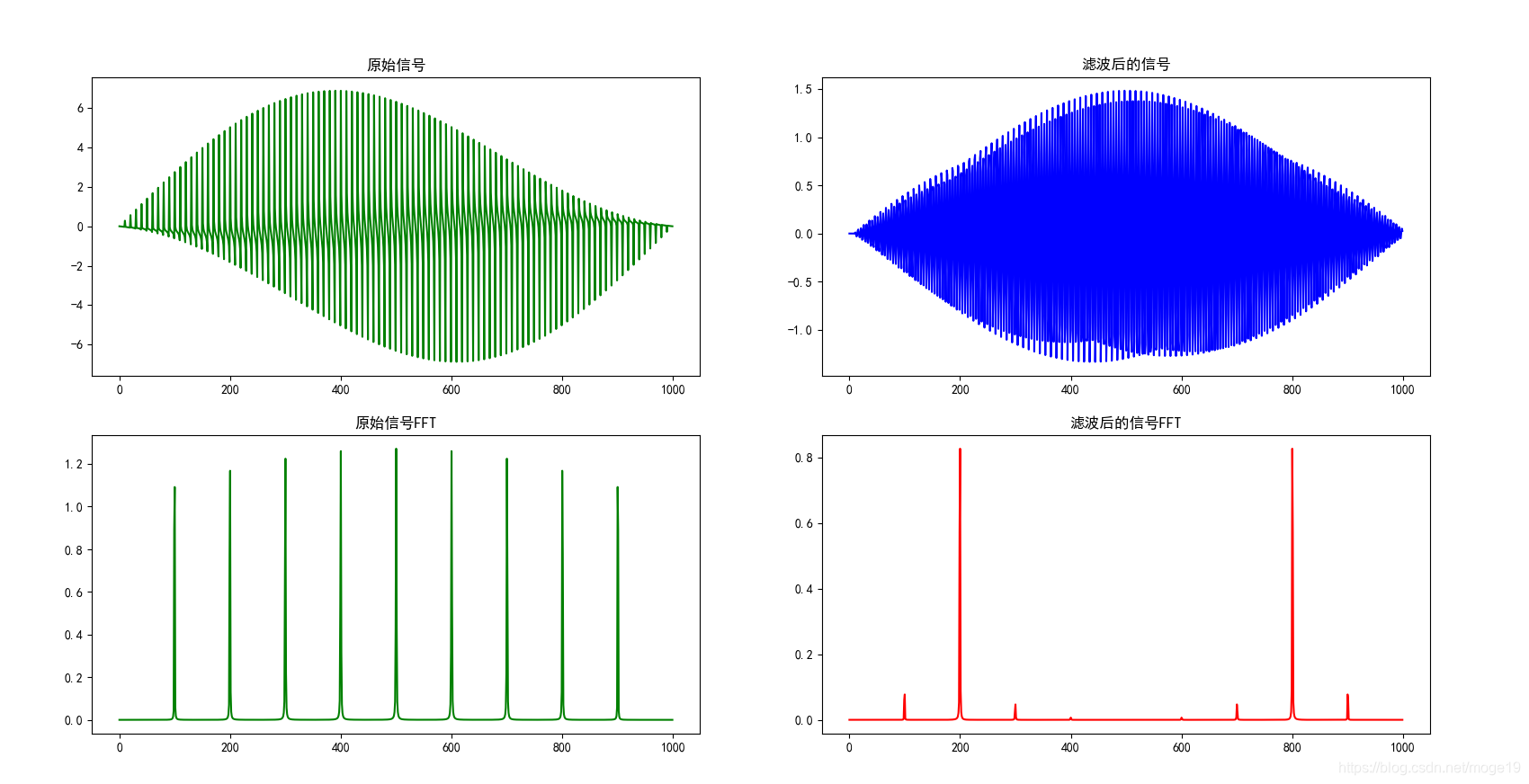
 可见滤波效果并不是特别好，若提高采样频率，将T=0.0001,得到如下结果：
 
                    1 巴特沃斯滤波设计步骤①归一化处理。即令λ=ω/ωpλ=ω/ω_pλ=ω/ωp②计算阶数，截止频率和通带频率比；ωsω_sωs是阻带截止频率，ωpω_pωp是通带截止频率,δsδ_sδs是阻带应达到的最小衰减λs=ωs/ωpλ_s=ω_s/ω_pλs=ωs/ωpN=log⁡(10(δs/10)−1)log⁡λsN=\frac{\log\sqrt{(10^{(δ_s/10)}-1)}}{log⁡λ_s }N=log⁡λslog(10(δs/10)−1)③构造归一化系统函数H
				本人本科渣渣一个，前两天导师让我设计一个数字滤波器。由于本人基本没有数字信号处理基础，于是只能依靠百度和matlab，折腾了半天总算是摸索明白了。百度上有一些文章不靠谱，很容易误导别人，故在此发一篇博客。
滤波器设计目标：设计一个1Hz截止频率的2阶低通巴特沃斯数字滤波器，并转化成C语言函数。（国标里提的要求）
滤波器指标：指标：截止频率Fc = 1Hz，阶数N=2，低通巴特沃斯滤波器
				Butterworth滤波器最先由英国工程师Stephen Butterworth于1930年发表在英国《无线电工程》期刊的名为“On the Theory of Filter Amplifiers”论文中提出。来自90余年前的古老智慧。
巴特沃斯滤波器在通带的频率响应曲线最平滑，其|H(jω)|^2在ω=0点的1至2N-1阶导数值为0，所以巴特沃斯滤波器也被称为也被称作最大平坦滤波器。
巴特沃斯低通滤波器的振幅平方对频率的公式为
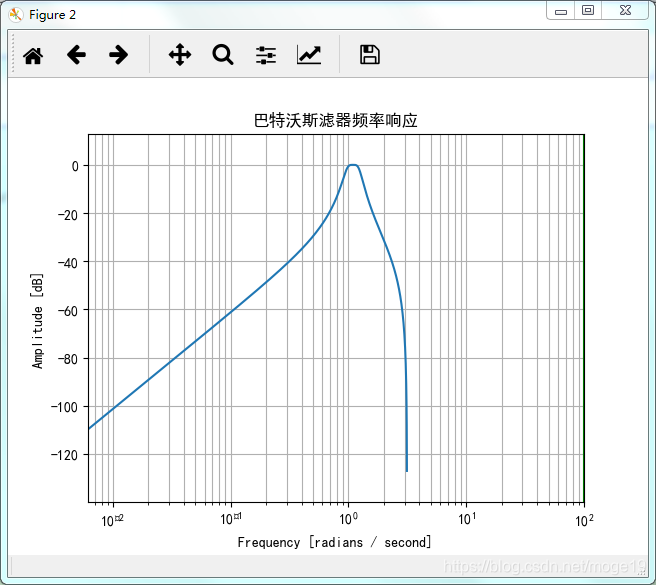
使用Python做出不同阶数的Butterworth滤波器的频率响应如下图
				心电信号去噪python
我妥协了实话实说，比起教程，这篇算是一个笔记吧，在我做心电的过程中，观察了一下心电相关的去噪方法，国内主要集中在应用中值滤波和小波变换，国外一般直接用一巴特沃斯了事。目前我只会应用，本来我是想理论都吃透了再写的，奈何类似小波之类的基本原理学起来实在一言难尽，说白了还是能力不够 ，等我再学一遍数字信号处理归来之日就是将理论补足之时。
1.巴特沃斯滤波器
1.1 巴特沃斯高通滤波
巴特沃斯滤波器是心电信号滤波最好用的滤波器，一个低频的高通滤波器可以去除基线漂移
比起我之前写了一整篇中值
				Python实现数字滤波器
文章目录Python实现数字滤波器1、IIR低通、高通、带通和带阻滤波器的设计1.1、设计滤波器的函数1.2、将滤波器应用于语音
由语音的产生和感知可知，基音频率的范围是60到450赫兹之间，故语音信号采集需要提取基音时，需要采用低通滤波器来获取低频基音信号，在采用计算机采集语音信号时，语音常混有50赫兹交流混音，也需要采用高通滤波器将其去除，此篇设计数字滤波器，以及实现他们在语言中的简单应用。滤波器传递函数如下：
给定数字滤波器的M阶分子b和N阶分母a：
				I have already got the data from the real robot, but the data is too wavy.
So I choose a filter same as the paper by my supervisor to obtain a smoother curve.
I use python to implement because my lear...
				#####################################
# 带通滤波，0.5~70hz  
#####################################
def butterBandPassFilter(lowcut, highcut, samplerate, order):
    "生成巴特沃斯带通滤波器"
    semiSampleRate = samplerate*0.5
    low = lowcut / semiSampleRate
    high = 
第五章：附录
第一章 整体思路
本次设计围绕四阶巴特沃斯低通滤波器，从电路设计，时域分析，频率分析，S域分析几个方面着手，通过理论分析、仿真实验、真实测量来研究和验证整个系统的性质。在时域上验证系统的冲激响应和阶跃响应以及零输入响应；在频域分析上验证系统的幅频曲线和相频曲线；在S域上通过极点分布研究系统是否稳定。
第二章 电路设计
1、运放芯片的选择
本次实验的截至频率不大于1KHZ，带宽不